This year, my project was about a very strange task: color mixing. I have to admit that at first, I thought that the most difficult and important part of my work would have been that of physical simulation of dripping and drying paint, and the simulation of the brush movements. How could mixing colors be so difficult?! Take their RGB values, and mix them additively or with some other simple transformation (the HSL color model is very useful, for example). But things are not so easy.
Color mixing is indeed a very difficult task. What is it exactly? It's about simulating what you learn at school: yellow and blue give green, red and yellow give orange... and so on. I have to simulate this behavior.
It's very difficult to explain the complexity in a few words, but it can be simplified this way: you can *not* know the final color of a mixture knowing only the RGB values of the components. So my work was: find a "color model" (that is, a way to represent colors) that has this property: the color of a mixture is the weighted sum of the values of the components.
Luckily, other people thought about this before me, in particular two researchers, Kubelka and Munk. They wrote a set of differential equations that describe (among other things) the behavior of pigments. The integration of these equations brings to another set, that permits the application to decide the color that would be viewed by mixing some components. Kubelka and Munk didn't see that their system has the property I was looking for: this discovery was made by Duncan, one of the guys that integrated their equations. His law states exactly what I was looking for: "the K and S values of a mixture are equal to the weighted sum of the K and S values of the components". K and S values stand for "Absorption" (K) and "Scattering (S). Again, it was not so easy to come to this: really, since the beginning I hoped that I could use some other systems instead of of Kubelka and Munk's one, because it's very complicated. I hoped that some simplifications were good enough to approximate the real behavior of paint without using their model.
At the end, it was evident that I could not escape from Kubelka and Munk, and so, I started implementing their theory. Many parts of it are very well documented: there is a good set of equations that permits transformation from K and S values to Reflectance values, and then from these to XYZ values, and from these to RGB values. Perfect! No, not exactly :-) Because I needed also exactly the opposite: a way to transform from RGB to K and S, and *then* viceversa :-) All papers I read gave K and S values as known, and didn't give me any hints on how to find them from RGB values.
Luckily again, after some search, I found a little, old paper that talked about this: the algorithm I found reading it isn't perfect, but it does work. I was able, after some (*much*) maths (thanks to Paolo Capriotti for his fuundamental help), to obtain these K and S values!
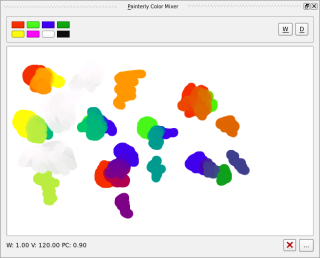
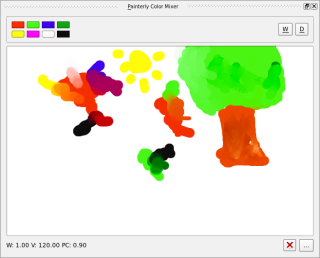
This happened just some days ago, when I committed the latest version of my mixer. Once I obtainted these values, finding the resulting color is really easy: just take the amount of paint for each component, and mix their K and S values proportionally to their presence... the final result is very realistic. For example, this model is the only way I found to obtain green from yellow and blue.
 |  |
 | |
Krita is the first public application that implements this technology. Only some other academic projects have managed this, and with a lot of CPU/GPU consumption (they need a cluster or a powerful GPU, or they would run only at very low resolutions). I suceeded in simplificating the process enough to run it on all machines I have, without using the GPU at all (and I have no clusters in my house :-)). Corel Painter doesn't do this (in fact, I guess that it can't mix as well as Krita now...), Photoshop doesn't do this.
With this technology, we can not only handle correct mixing from RGB values, but also the creation of *real* colors (that is, color defined not only by their RGB values, but also by their "Reflectance", that's the main and fundamental property that gives a color its... color); we can handle illumination, that is: changing the virtual light that illuminates the scene will change the colors present in it. A very good set of features, they are not implemented yet but the infrastructure is here.
 KDE Commit-Digest
KDE Commit-Digest